从 SIR 模型到基于智能体的模拟 —— 新冠肺炎的传播演化可视化
校对:
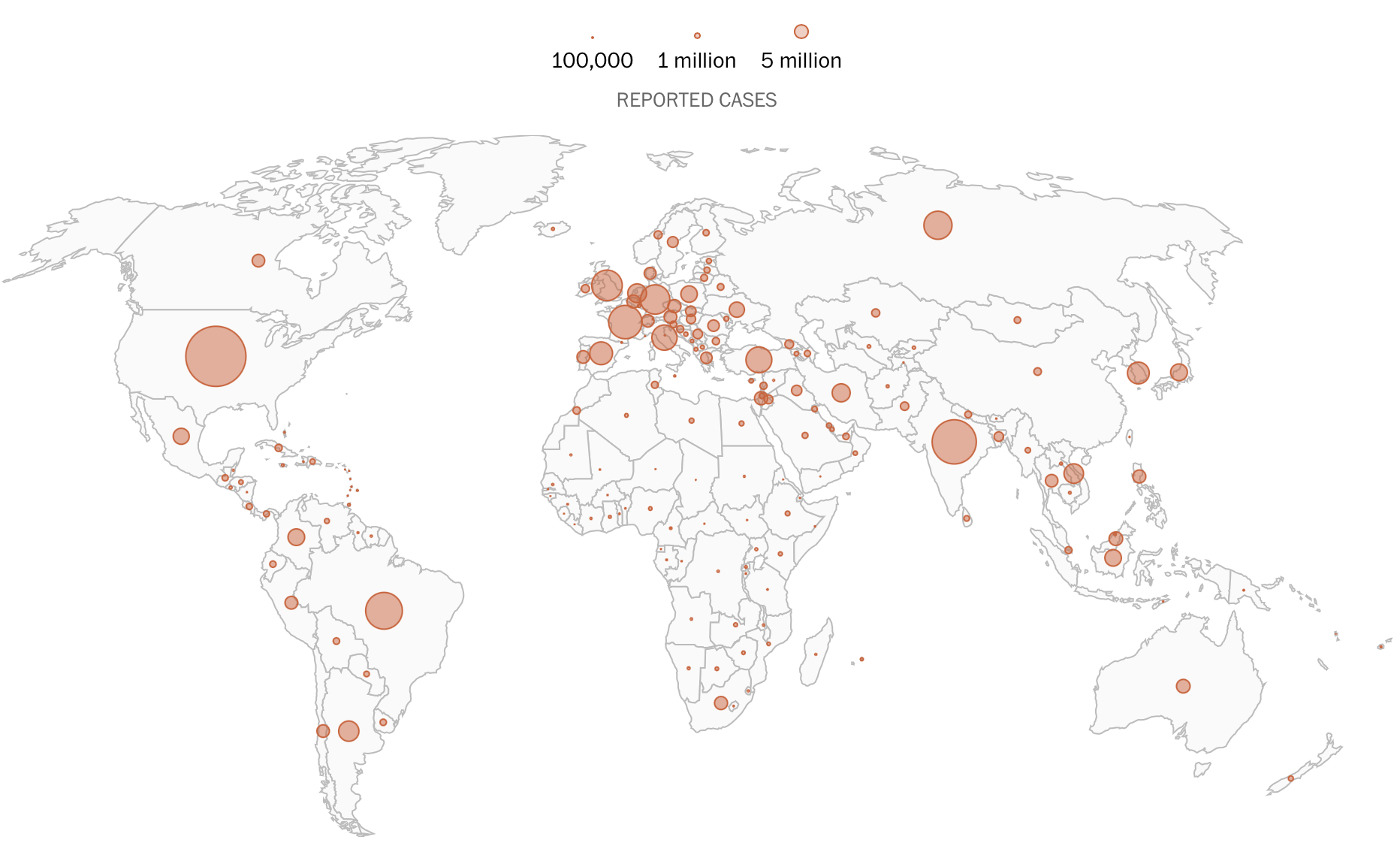
自 2019 年底首次发现新型冠状病毒以来到现在,已经有超过 500多万人在这场大灾难中死亡,并且有超过 25 亿的新冠病例被报告(数据来自约翰-霍普金斯大学)。由于最近新冠病毒的变种带着极强的传染力通过旅行者甚至快递包裹向国内发起进攻,导致国内多地疫情频发,隔离、核酸检测、快递停发、居家办公频频出现在微博热搜。我们的脑中不禁会想到,疫情是如何传播的?为何疫情的「拐点」经常被提及?为何疫情迟迟得不到控制?为何中国的防疫成果这么优秀?作为一个好奇宝宝,怎么能不细细的探索一番,因此笔者在 Beach 的闲暇时间做了一个新冠疫情的传播模拟 Demo,和大家一起理解疫情传播的演化。
太长不看
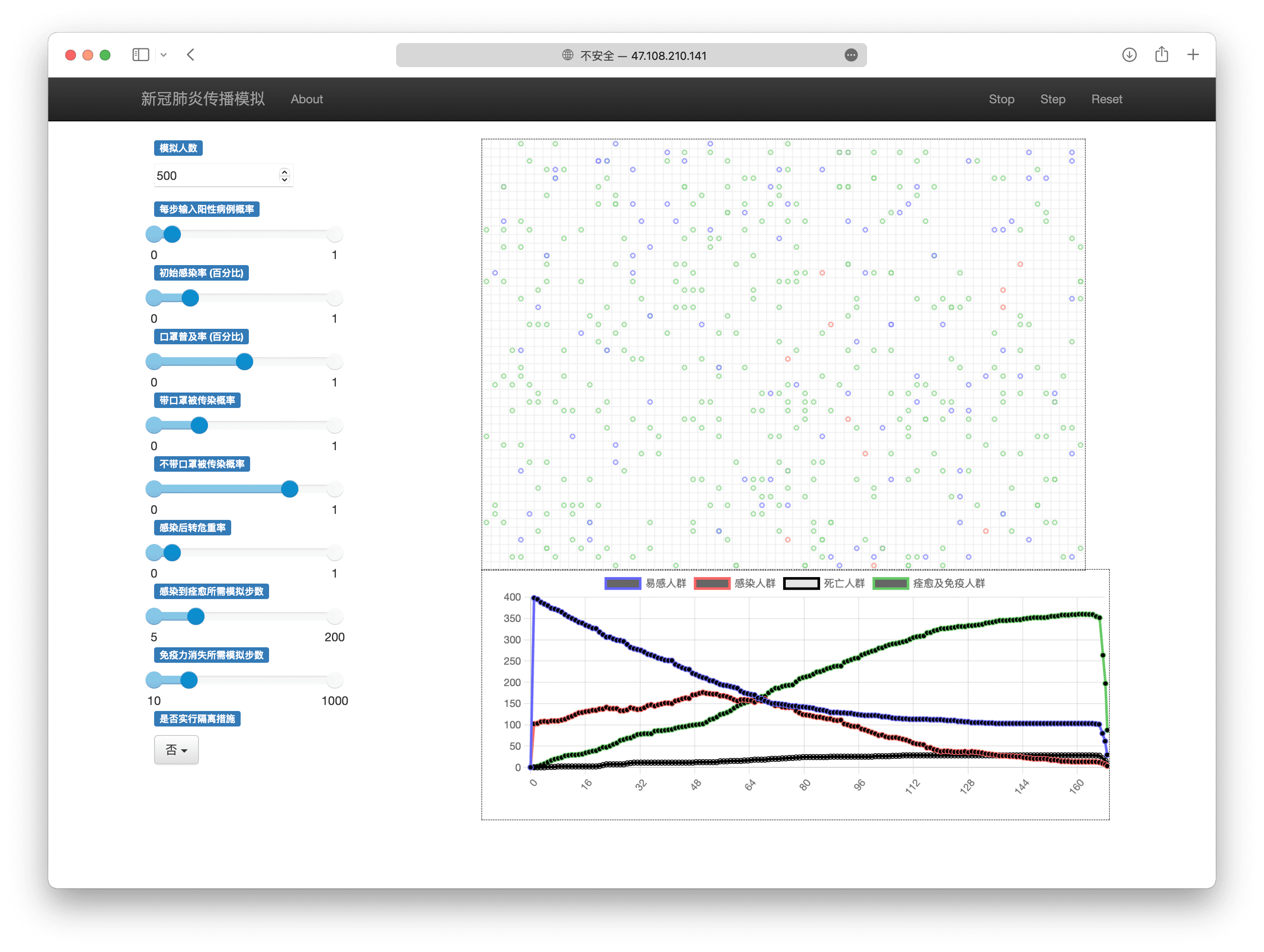
受 SIR-F 模型启发,笔者使用 Mesa 开发了一个新冠疫情的传播模拟 Demo,如下方视频所示,左边栏可用于调整模拟参数,右上角的网格将展示人群(小圆)移动情况以及感染状态;右下角对不同人群的总数进行动态显示。
Show me the code
Show me the demo
该 demo 基于 WebSocket 进行前后端传输,需要消耗大量网络带宽(服务搭在一个廉价服务器上,最大带宽只有 1M 🤕),如果遇到模拟过程卡顿,请暂时关闭稍后再试,谢谢~
 https://bramble-palladium-8dd.notion.site/SIR-65d2a63368494539a7587e9ffe2235f1
https://bramble-palladium-8dd.notion.site/SIR-65d2a63368494539a7587e9ffe2235f1
SIR 模型及其变体
SIR 模型是一个用来理解疾病爆发的简单数学模型,由 Kermack 与 McKendrick 在 1927 年研究流行于伦敦的黑死病的时候提出,本文将首先对 SIR 模型进行一些简要的解释。
- : Susceptible 易感者 (= 总人口数 - 确诊人数)
- : Infected 感染者 (= 确诊人数 - 治愈人数)
- : Recovered 治愈且有免疫力者 (= 治愈人数)
该模型可以简单表示为
给出该模型的常微分方程:
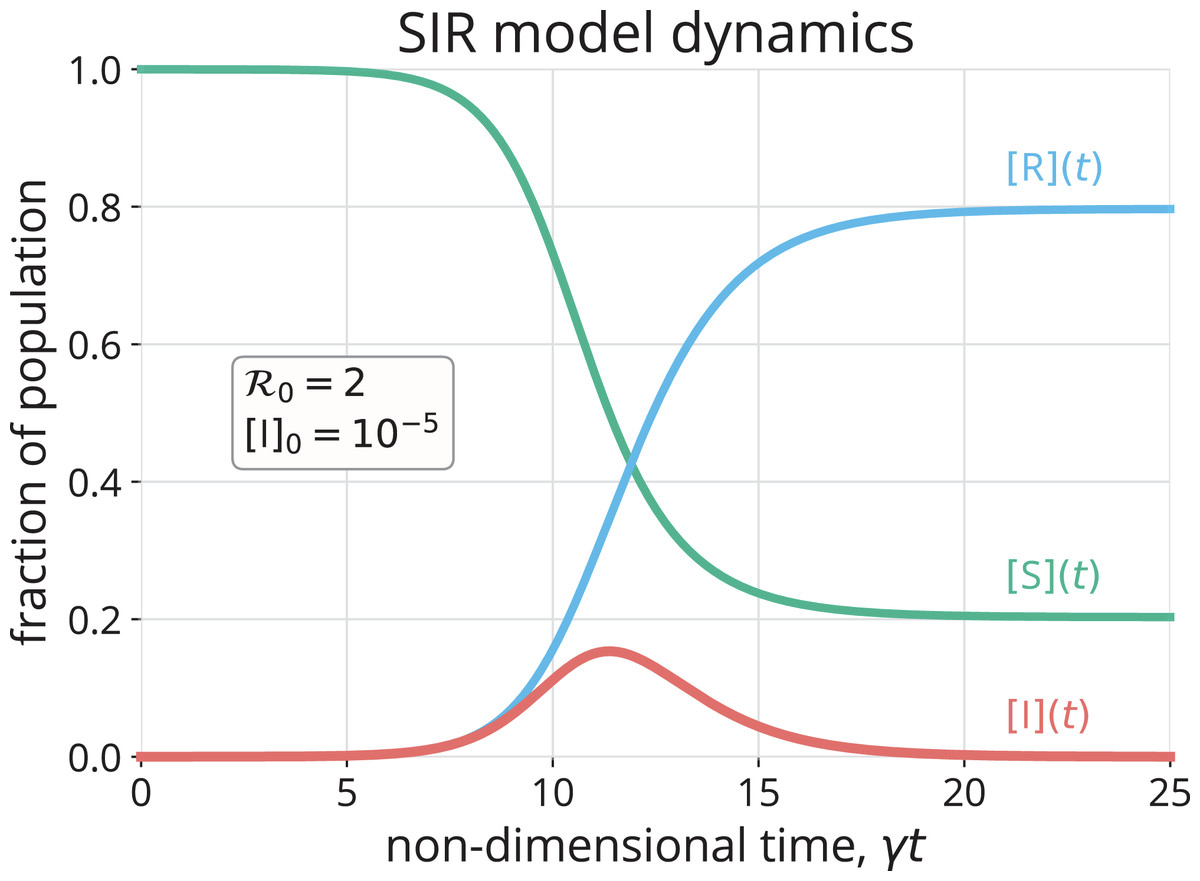
其中总人口数 , 是疫情开始到当前经过的时间,图 2 给出了一个常见的 SIR 模型模拟结果,其中绿、红、蓝色三条线分别代表易感人群、感染者人群以及治愈者的数量随时间的变化。从图中我们可以发现,在第 11 个单位时间的时候,感染者数量最多,感染速率和治愈速率相等,表示疫情已经进入平稳阶段。
结合实际的模拟实验和生活经验,可以发现这个简单模型并不能很好的对新冠病毒的爆发进行建模,首先它没有考虑重症造成的大量死亡会显著影响易感人群的数量。此外,在新冠爆发的初期,许多人是在死后才确诊,病毒的确诊滞后也会影响病毒的扩散以及正确的估计。
针对新冠肺炎进行调整的 SIR-F 模型
针对上述问题,LISPHILAR 结合新冠肺炎病毒的传播规律以及真实的临床表现提出了 SIR-F 模型对新冠爆发进行模拟,他定义:
- : 易感者 (= 总人口数 - 确诊人数)
- : 新冠阳性但并没有被发现
- : 新冠阳性且被发现
- : 新冠阳性但已经痊愈
- : 新冠阳性且重症 (Fatal)
其中, 指的是那些携带病毒但并没有人(包括他们自己)知道的病例,他们可能在死亡后被确认为是新冠阳性,也有可能之后会被确认然后转为感染者。我们知道新冠确诊而死亡的病例数,但我们不知道没有确诊就死亡的病例数。本质上, 作为 SIR-F 模型的一个辅助区间,将两种死亡情况分开,并插入一个属于 区间的概率因子。
变量之间的关系:
确诊数量 =
痊愈数量 =
死亡人数 =
其常微分方程的表达式就是:
其中,总人口 , 是疫情开始到当前经过的时间。
除了上述模型以外,还有类似 SEIR 等 SIR 模型的变体,这里不再赘述。 SIR 系列模型能够用于估计疫情在不断时刻的态势以及最终的结局,评估疫情造成的影响,还可以指导管理者对疫情的传播进行干预以尽量降低真实的损失。此类模型目前还是存在许多局限性,该模型需要输入大量根据历史数据或者经验得出的参数,例如有效接触比例、阳性确诊比例等,其对人群的分类也比较简单,理想化的传播过程也难以表达现实环境对传播的影响,预测结果与真实数据会存在偏差。目前全世界的研究人员也在持续探索更加科学、准确的传染病传播建模方法。
受 SIR-F 模型启发的新冠肺炎传播模拟
SIR-F 模型可以看作是一个宏观模型,用于抽象的描述传染病的传播过程,能够帮助分析者直接发现这些统计数据的趋势。相对的,基于智能体的建模方法(Agent-based Model)作为一种模拟方法,强调单个代理的行为,是一种更灵活、更细化的自下而上方法,可以捕获宏观模型无法捕获的细节。智能体可以用来代表活细胞,动物,个人,甚至整个组织或抽象实体。
我们可以使用基于智能体的建模方法对人们的活动、互动以及病毒在人们之间的传播进行模拟。假设分析者想预测特定地区的新冠肺炎病例数,可以创建一些智能体来代表该地区的居住者。同样,还可以模拟智能体(人)的行为,其中一些人出门都会戴口罩,而另一些人不会,一些人非常喜欢社交,而另一些人则喜欢宅家等等。然后我们可以模拟他们彼此之间的交互以及病毒传播相关的概率……
运行模拟后,分析者能够更好地了解整个系统,从中可以看到人群中的感染人数、治愈人数、传播率、是否达到群体免疫等。我们还可以看到疫情在整个区域的演化过程,从而帮助分析者找到防止疫情扩散的方法以及执行这些方法所带来的成果。这种基于智能体的建模方法的基石是从微观行为中理解归纳宏观现象的能力,在生物学、社会科学、交通管理和供应链管理等许多学科中都有应用。
受 SIR-F 模型启发,笔者使用 Mesa 开发了一个新冠疫情的传播模拟 Demo,如图 3 所示,左边栏用于调整模拟参数,右上角的网格将展示「人群」移动情况以及感染状态;右下角对不同人群的总数进行动态显示。
基于智能体的模拟框架 Mesa
Mesa 是一个用于构建,分析和可视化基于智能体的模型的模块化开源框架,该框架基于 Python 3 开发,一方面能够助力研究系统的整体行为,还适合用于各种模型智能体的合作与竞争关系的研究。它允许用户使用内置的核心组件(如二维网格和智能体调度器)或定制的实现函数快速创建基于智能体的模型;使用基于浏览器的界面将模拟的结果可视化;并使用 Python 的数据分析工具分析其结果。在用户设计好了模拟规则运行模型之时,它会创建一个基于 Tornado 的服务器程序,通过 WebSocket 实时传输模拟结果到前端进行可视化呈现。
模型配置
笔者将使用 Mesa 框架来模拟新冠肺炎在一个固定区域内的传播。假设有一个 70 x 50 的网格,网格内有 350 个格子用来代表空间位置,网格中还有能够在格子中自由移动的智能体,他们能够接触,接触的时候可能会传染病毒。
受到 SIR-F 模型的启发,这里对模型做了如下假设以及规则:
- 系统会初始化用户设置数量的智能体,这些智能体一开始会被分配到网格中的随机单元格,每个单元格可以存在多个智能体。
- 智能体在每一步中要么保持不动,要么移动到上下左右相邻的单元格。
- 系统能够通过可设置参数控制所有智能体在整个模拟过程中戴口罩以及不带口罩的比例
- 系统能够通过可设置参数控制智能体在被感染后罹患轻症或重症的比例,重症在感染后的每一天都会有一定概率死亡,死亡后的智能体将被移出网格,而轻症一定不会死亡。
- 当易感者与另一个感染者在同一个格子中时,它们会根据戴口罩和未戴口罩相应的传染概率(可设置参数)判断是否被感染。
- 如果一个智能体被感染,它会在一定数量的模拟步骤(可设置参数)后治愈并获得免疫能力。
- 经过一定数量的步骤(可设置参数)后智能体的免疫力消失,并且会再次变得易感。
- 为了使模型更加适配国内的情况,笔者还加入了隔离政策,如果隔离政策启用,那确诊病例将大概率不能在网格移动并且失去传染力(因为屏蔽了物理接触)。
- 此外,该模型还会简单的考虑境外输入感染者的情况,用户可以设置每一步出现境外输入传染者的概率,新的被感染智能体将被随机分配网格中。
视觉配置
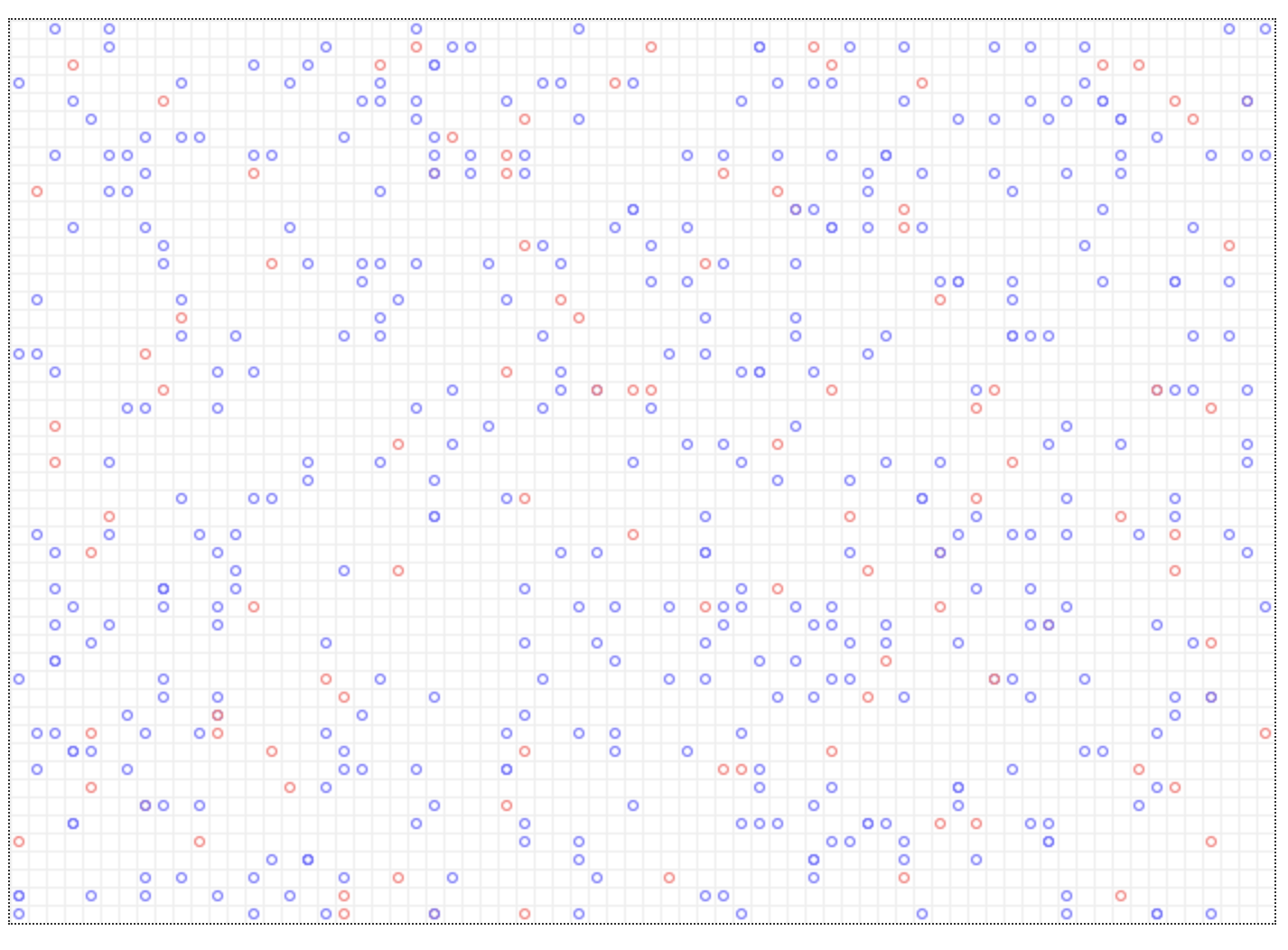
如图 4 所示,网格被放置在系统的右上方,每个智能体都被表示为网格中的一个小圆。其中易感者着紫色,感染者着红色,治愈的和具有免疫能力的着绿色,重症患者将被移出该网格。系统右下方的图表将使用相应颜色的线条实时记录各类人群的总数。
不同参数的模拟结果对比
通过设置不同的参数,可以模拟当前各个国家的疫情演化情况,下面两个案例都设置了同样的新冠感染概率以及初始传染者的比例,唯一不同的是是否施行隔离措施。
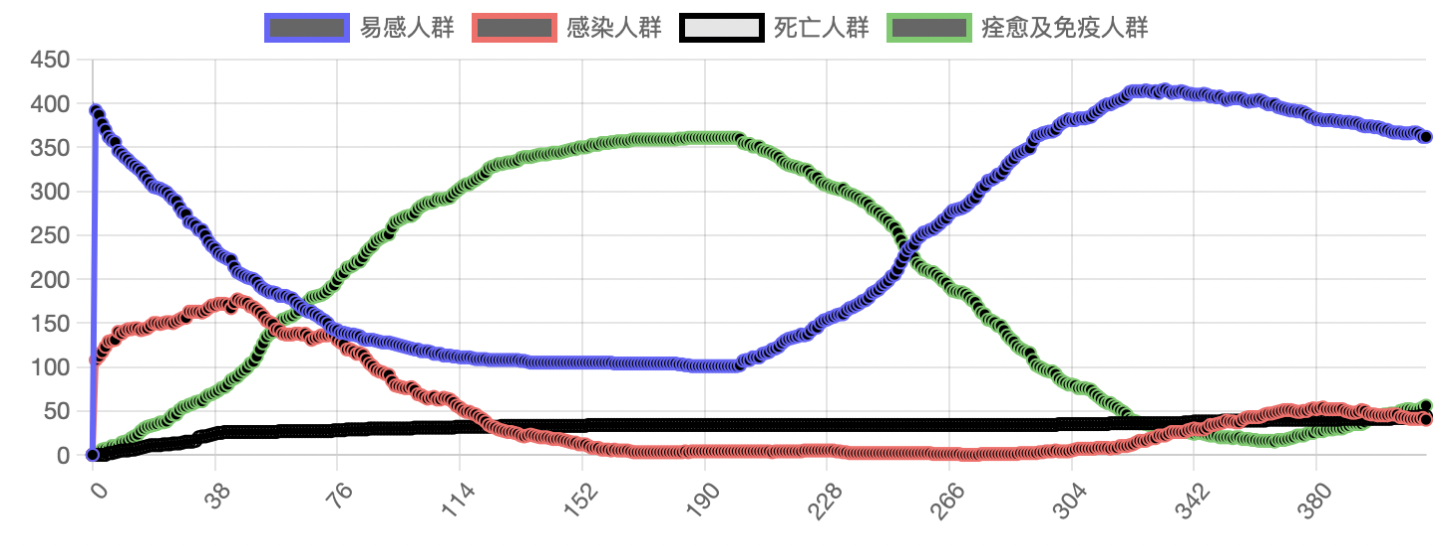
例如「某个国家」没有施行隔离政策,并且完全允许其他国家的新冠阳性或未被检出的新冠阳性患者进入国家。这个国家的疫情传播趋势就会像图 5 一样,疫情将会在 190 天的时候基本没有新增阳性案例,但是在 304 天由于境外的输入,该国的疫情死灰复燃,在第 380 天也就是模拟的最后一天,死亡率在 10 % 左右。
而在另外的一些国家,例如中国,政府施行严格的隔离政策,并且严格限制入境的人数以及不允许感染者入境。这个国家的疫情传播趋势就会像图 5 一样,疫情将会在 90 天的时候基本没有新增阳性案例,在 280 天所有的治愈人群都重新变成了易感人群,在第 340 天的时候死亡率在 1 % 左右。
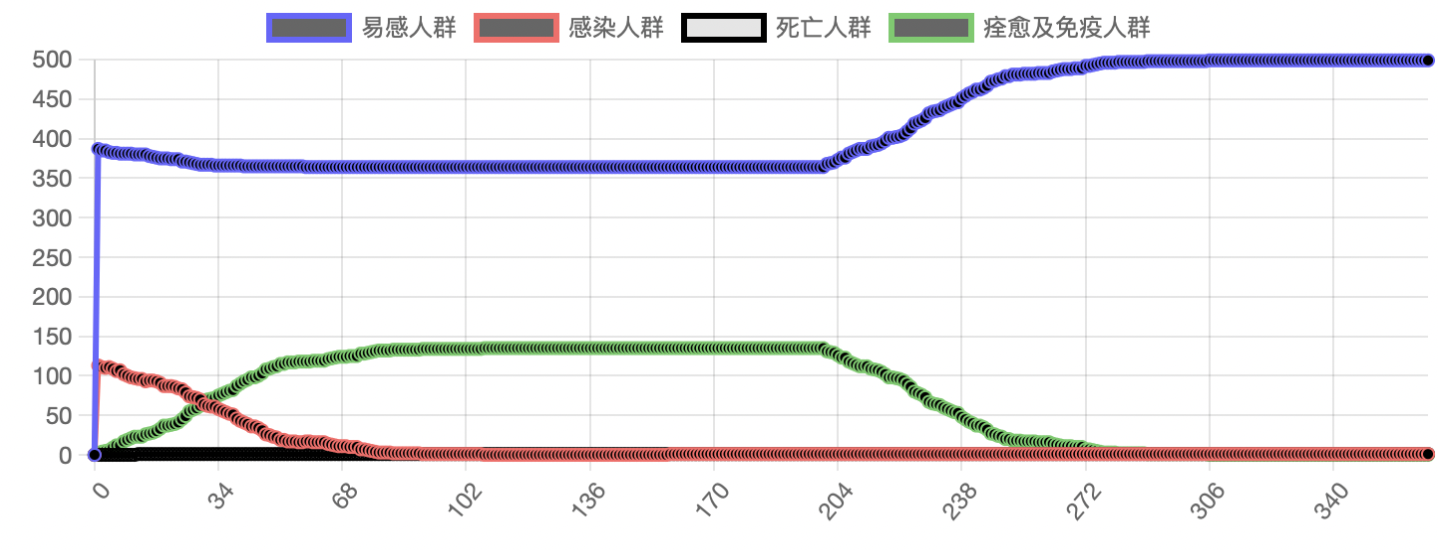
对图 5 和 图 6 的曲线趋势,可以发现差异是很明显的,这也说明了一些国家放任不管,企图用全民免疫来减少经济危机需要承担多么严重的后果。
延伸阅读
如果对疫情传播模拟或者可视化感兴趣的小伙伴可以访问下面的资料了解更多关于疫情模拟以及可视化的知识。
疫情传播可视化
EpiMob: Interactive Visual Analytics of Citywide Human Mobility Restrictions for Epidemic Control [link]
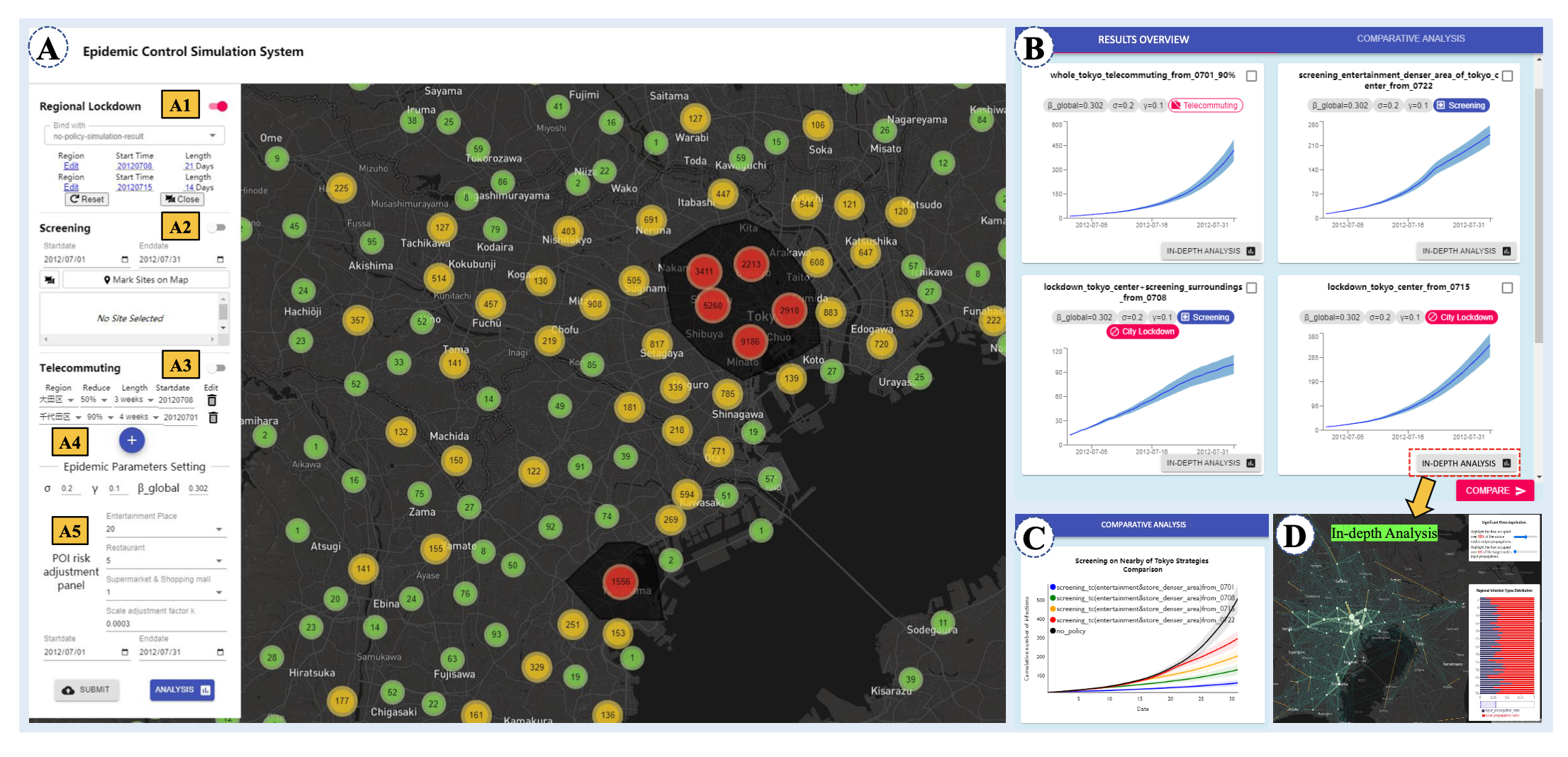
EpiMob 系统能够交互式模拟在实施某种限制政策或政策组合(如区域封锁、远程办公、核酸筛查)的情况下,人类流动性和感染者数量的变化。使用者可以方便地指定流动限制政策应用的时空范围,相应的感染模拟情况能够被动态显示。
McKinsey & Company, Tracking the impact of COVID-19 [link]
麦肯锡针对新冠疫情追踪设计的一系列交互式可视化,旨在为如何在 COVID-19 危机中保护生命和维持生计等提供有效信息。

疫情传播模拟方法
How simulation modelling can help reduce the impact of COVID-19 [link]
文章 2.2 节详细论述了能够用于新冠疫情模拟的四种建模方法,并在第 3 章总结了这四种方法的优缺点。
Crowding and the shape of COVID-19 epidemics [link]
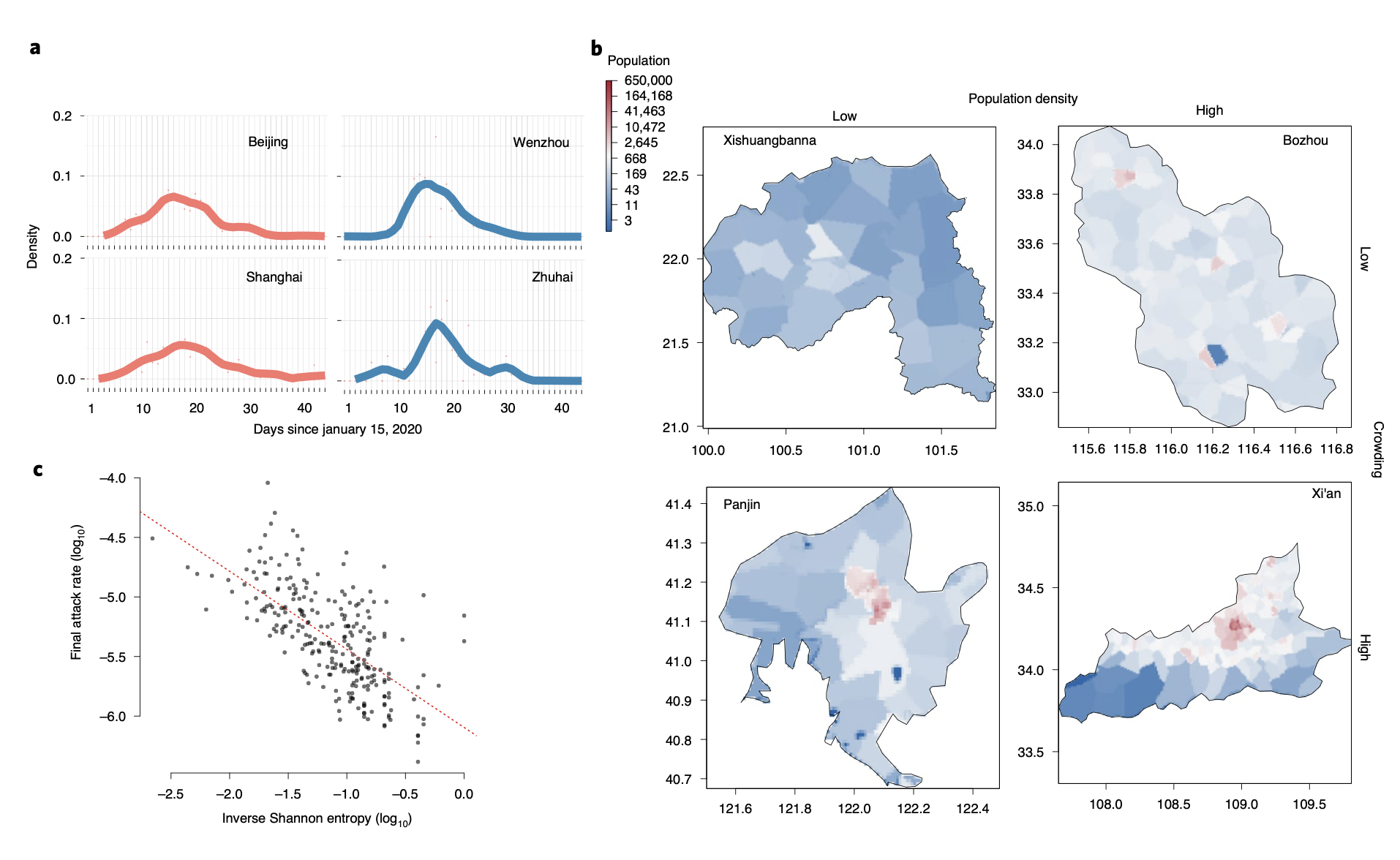
文章作者发现在国家内部和国家之间,COVID-19 病例的地理分布存在着明显的差异。他们发现,其中一些差异是由于人口拥挤的空间变化造成的。他们对比中国和意大利城市间 COVID-19 的详细病例计数数据,他们发现,拥挤程度较高的城市在第一波疫情发生后,流行时间更长。
新冠病毒变异情况
Genomic epidemiology of SARS-CoV-2 with global subsampling [link]
这是一个利用病原体基因组数据为科研以及公共卫生提供辅助的项目,能够了解当前新冠病毒的变异情况以及各种变体的衍生子类出现的时间以及占比。
写在最后
在最后衷心的希望疫情早点结束,完成自己的旅行清单,每天都能见到自己想见的人。
送大家一首歌。
🎵🎵🎵 新冠,请滚出这个地球 🎵🎵🎵
参考资料
Bassel Karami, Intro to Agent Based Modeling
Bassel Karami, Agent-Based Model Visualization
LISPHILAR, COVID-19 data with SIR model
WIKIPEDIA, Compartmental models in epidemiology
本文使用 Notion 编辑